 | Сервис для решения задач по линейному программированиюи другие интересные типовые задачи |
English |
Пример №5. Решение задачи линейного программирования графическим методом.
Функция достигает наибольшего значения на луче
F = - x1 + x2
при следующих ограничениях:
| x1 | - | 2 x2 | ≤ | 4 | ||
| x1 | - | x2 | ≥ | 1 | ||
| x1 | + | x2 | ≥ | 2 |
x1 ≥ 0 x2 ≥ 0
Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.
Очевидно, для нахождения области допустимых решений данной задачи, необходимо последовательно рассмотреть каждое неравенство. (см. шаг 1 - шаг 3)
Последние два шага служат непосредственно для получения ответа. (см. шаг 4 - шаг 5)
Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.
Посмотреть план решение этой задачи в картинках
По условию задачи: x1 ≥ 0 x2 ≥ 0.
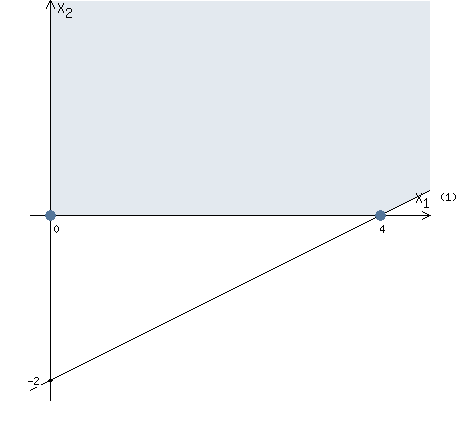
Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).
Рассмотрим неравенство 1 системы ограничений.
x1 - 2 x2 ≤ 4
Построим прямую: x1 - 2 x2 = 4
Пусть x1 =0 => - 2 x2 = 4 => x2 = -2
Пусть x2 =0 => x1 = 4
Найдены коородинаты двух точек (0, -2) и (4 ,0). Соединяем их и получаем необходимую прямую (1).
Нас интересуют точки расположенные выше или ниже построенной прямой (1) ?
Вернемся к исходному неравенству.
x1 - 2 x2 ≤ 4
Преобразуем неравенство, оставив в левой части только x2
- 2 x2 ≤ - x1 + 4
x2 ≥ 1/2 x1 - 2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (1).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 2 системы ограничений.
x1 - x2 ≥ 1
Построим прямую: x1 - x2 = 1
Пусть x1 =0 => - x2 = 1 => x2 = -1
Пусть x2 =0 => x1 = 1
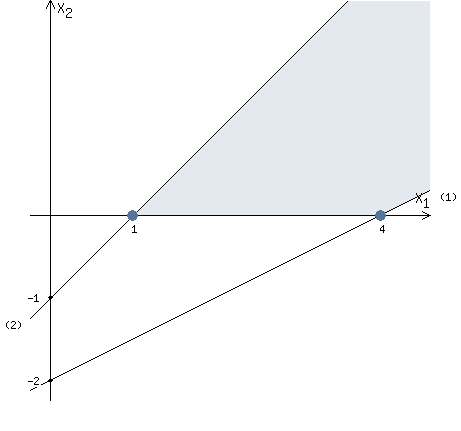
Найдены коородинаты двух точек (0, -1) и (1 ,0). Соединяем их и получаем необходимую прямую (2).
Нас интересуют точки расположенные выше или ниже построенной прямой (2) ?
Вернемся к исходному неравенству.
x1 - x2 ≥ 1
Преобразуем неравенство, оставив в левой части только x2
- x2 ≥ - x1 + 1
x2 ≤ x1 - 1
Знак неравенства ≤ . Следовательно, нас интересуют точки расположенные ниже построенной прямой (2).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
Рассмотрим неравенство 3 системы ограничений.
x1 + x2 ≥ 2
Построим прямую: x1 + x2 = 2
Пусть x1 =0 => x2 = 2
Пусть x2 =0 => x1 = 2
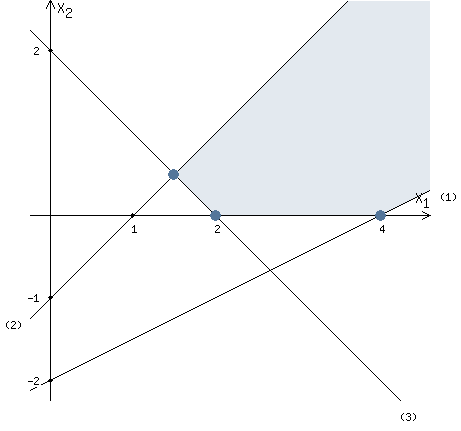
Найдены коородинаты двух точек (0, 2) и (2 ,0). Соединяем их и получаем необходимую прямую (3).
Нас интересуют точки расположенные выше или ниже построенной прямой (3) ?
Вернемся к исходному неравенству.
x1 + x2 ≥ 2
Преобразуем неравенство, оставив в левой части только x2
x2 ≥ - x1 + 2
Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (3).
Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.
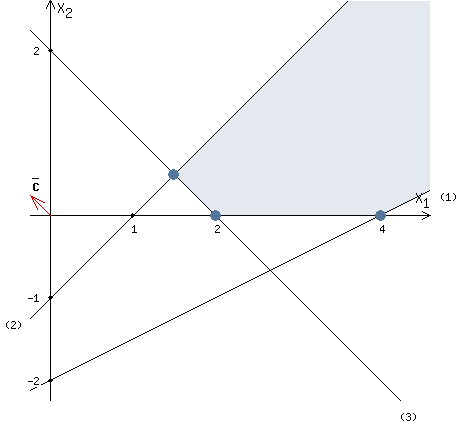
Строим вектор C = (-1, 1), координатами которого являются коэффициенты функции F.
Вектор C нарисован не в масштабе, так как он не помещается на рисунке.
Будем перемещать "красную" прямую, перпендикулярно вектору C, от правого нижнего угла к левому верхнему.
"Красная" прямая называется линией уровня. В каждой точке линии уровня значение функции F есть величина постоянная.В точке, в которой "красная" прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.
В точке, в которой "красная" прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.
Есть предположение, что функция F достигает наибольшего значения на луче, который имеет свое начало в точке А (см. рисунок).
Проверим это предположение.
Найдем координаты точки A.
Точка A одновременно принадлежит прямым (2) и (3).
| x1 | - | x2 | = | 1 | => | x1 = 3/2 | ||
| x1 | + | x2 | = | 2 | x2 = 1/2 |
Вычислим значение функции F в точке A (3/2,1/2).
F (A) = -1 * 3/2 + 1 * 1/2 = -1
На основании уравнения прямой (2) на которой находится луч, имеющей свое начало в точке А, можно записать параметрическое уравнение луча следующим образом:
x1 = 3/2 + 1 * t
x2 = 1/2 + 1 * t
где t ≥ 0
Предположим, что при t = 1 мы имеет точку В.
Найдем координаты точки B.
x1 = 3/2 + 1 * 1 = 5/2
x2 = 1/2 + 1 * 1 = 3/2
Вычислим значение функции F в точке B (5/2,3/2).
F (B) = -1 * 5/2 + 1 * 3/2 = -1
F(A) = F(B)
Тогда можно сделать вывод, что и в любой точке луча, имеющего свое начало в точке А, функция F достигает своего наибольшего значения.